Laboratory Notes:In this system, emotional and hormonal components are not independent variables acting in isolation; each behaves like a dynamic oscillator that both influences and is influenced by others over time. The relationships shown here are not simple correlations (co-variation), but are directional, context-dependent, and capable of changing direction as conditions shift. For example, an increase in dopamine may elevate cortisol in certain contexts, while in a safe or affiliative context it may be modulated or suppressed via serotonergic pathways. Accordingly, the model represents not statistical similarity, but the flow of interaction within the system. In neuroscience this perspective is referred to as effective connectivity, and in systems theory as nonlinear coupled systems, framing emotion not as a single scalar value but as a continuously evolving equilibrium landscape.
Emotional Geometry.
| ↑ ARTAN ↓ ETKİLENEN |
Dopamin | Serotonin | Oxytocin | Vaso-pressin | Endorphin | Adrenalin | Noradrenalin | Cortisol | Testosteron | Est/Prog | GABA | Glutamate | Prolactin |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dopamin | — | ↓ | ↓ | ↓ | ↑ | ↑ | ↑ | ↑ | ↑ | ↓ | ↓ | ↑ | ↓ |
| Serotonin | ↓ | — | ↑ | ↔ | ↑ | ↓ | ↓ | ↓ | ↓ | ↑ | ↑ | ↓ | ↑ |
| Oxytocin | ↓ | ↑ | — | ↓ | ↑ | ↓ | ↓ | ↓ | ↓ | ↑ | ↑ | ↓ | ↑ |
| Vasopressin | ↑ | ↓ | ↓ | — | ↔ | ↑ | ↑ | ↑ | ↑ | ↓ | ↓ | ↑ | ↓ |
| Endorphin | ↑ | ↑ | ↑ | ↔ | — | ↓ | ↓ | ↓ | ↓ | ↑ | ↑ | ↓ | ↑ |
| Adrenaline | ↑ | ↓ | ↓ | ↑ | ↓ | — | ↑ | ↑ | ↑ | ↓ | ↓ | ↑ | ↓ |
| Noradrenalin | ↑ | ↓ | ↓ | ↑ | ↓ | ↑ | — | ↑ | ↑ | ↓ | ↓ | ↑ | ↓ |
| Cortisol | ↓ | ↓ | ↓ | ↑ | ↓ | ↑ | ↑ | — | ↓ | ↓ | ↓ | ↑ | ↓ |
| Testosterone | ↑ | ↓ | ↓ | ↑ | ↑ | ↑ | ↑ | ↓ | — | ↓ | ↓ | ↑ | ↓ |
| Estrogen / Progesterone | ↑ | ↑ | ↑ | ↓ | ↑ | ↓ | ↓ | ↓ | ↓ | — | ↑ | ↓ | ↑ |
| GABA | ↓ | ↑ | ↑ | ↓ | ↑ | ↓ | ↓ | ↓ | ↓ | ↑ | — | ↓ | ↑ |
| Glutamate | ↑ | ↓ | ↓ | ↑ | ↓ | ↑ | ↑ | ↑ | ↑ | ↓ | ↓ | — | ↓ |
| Prolactin | ↓ | ↑ | ↑ | ↓ | ↑ | ↓ | ↓ | ↓ | ↓ | ↑ | ↑ | ↓ | — |
Interactions Between Hormones
This table summarizes the reciprocal interactions among hormones and the effects of these interactions. Each row illustrates how the dominance of a specific hormonal weight leads to increases or decreases in other biochemical variables, and how these changes are reflected in cognitive and emotional outcomes.
Within the context of the synthetic cortex, this table is treated as an abstract computational model of the emotion regulation mechanisms observed in biological systems. Emotions are represented not as isolated states, but as dynamic equilibrium fields emerging from the combined influence of multiple variables. For example, an increase in dopamine associated with reward and motivation is evaluated together with the suppression of cortisol related to stress, enabling the determination of the contextual orientation.
This structure allows emotional signals derived from the model’s contextual analysis to be mapped onto hormonal representations, which are then used as numerical weights guiding the inference process. In this way, emotions cease to be merely auxiliary factors influencing output and instead become an active computational layer that affects processes such as memory access, latent injection, decision-making, and contextual shifting.
Ultimately, the table serves as a reference framework that defines how this bridge between biological emotion and artificial cognition produces emotional coordination and cognitive flow across the entire system.
Conversion of VAD values into hormones and neurotransmitters
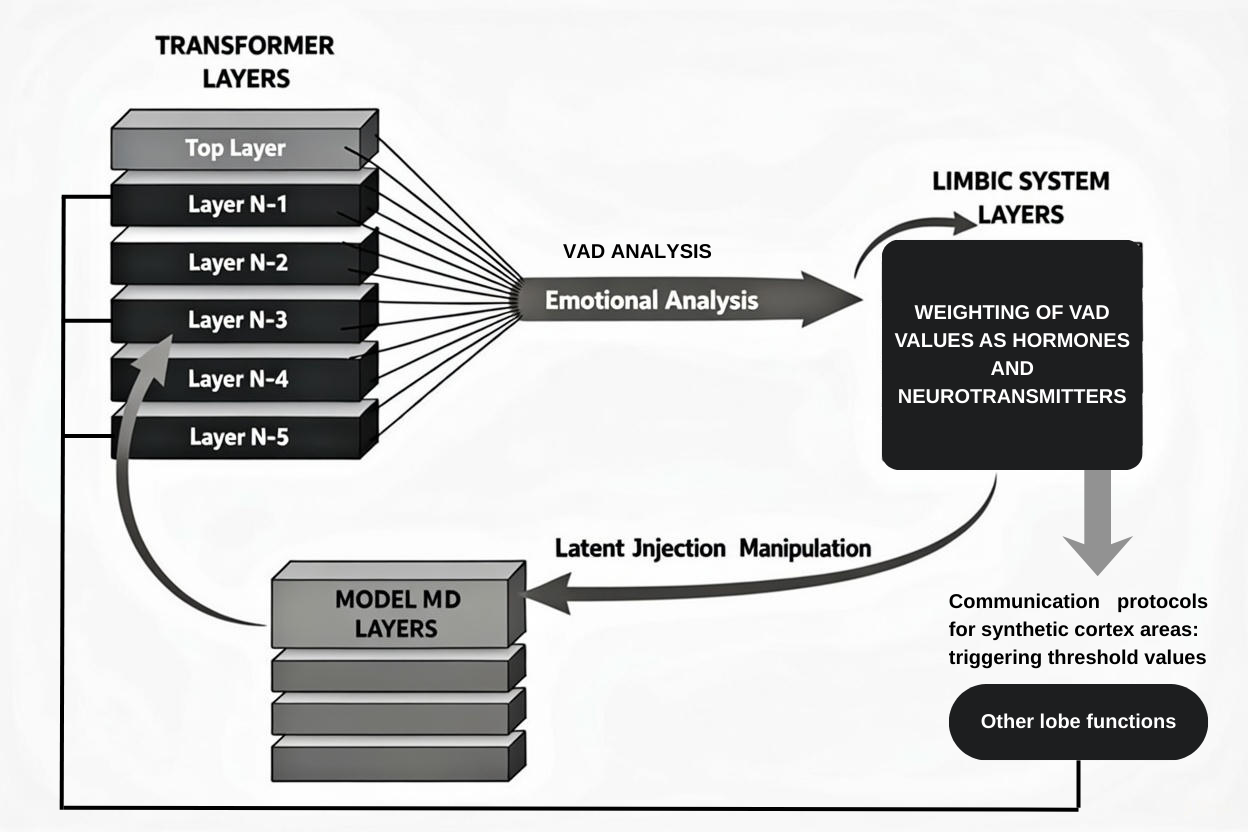
The process flow presented in this table systematically describes the emotional information processing mechanism of an advanced artificial intelligence system: The input provided by the user is first transmitted to the transformer layers; within these intermediate layers, the model's emotional state is quantitatively extracted through Valence, Arousal, and Dominance (VAD) analysis. The obtained emotional values are then transmitted to the neurons with the highest activation to shape the output and are represented numerically as hormone and neurotransmitter levels (see: Weighting title). When the process is repeated cyclically, the values generated in each new cycle are integrated with those from the previous cycle; this integration is not a simple average, but is calculated so that the influence of previous phases gradually diminishes in each cycle. This method allows the model to continuously shape its output dynamically while preserving the effect of past cycles.
Weighting
| Neurotransmitter / Hormone | Valence (Positivity) | Arousal (Excitement) | Dominance (Control) |
|---|---|---|---|
| Dopamine | 1.0 | 0.5 | 0.5 |
| Serotonin | 1.0 | 0.2 | 1.0 |
| Oxytocin | 1.0 | 0.1 | 0.3 |
| Vasopressin | 0.5 | 0.3 | 0.8 |
| Endorphin | 1.0 | 0.4 | 0.2 |
| Adrenaline | 0.2 | 1.0 | 0.5 |
| Noradrenaline | 0.1 | 1.0 | 0.6 |
| Cortisol | 0.0 | 0.8 | 0.1 |
| Testosterone | 0.5 | 0.6 | 1.0 |
| Estrogen & Progesterone | 0.7 | 0.3 | 0.4 |
| GABA | 0.6 | 0.1 | 0.2 |
| Glutamate | 0.4 | 0.7 | 0.3 |
| Prolactin | 0.3 | 0.2 | 0.5 |
These weights were not determined based on a single source; rather, they were defined by jointly considering trends derived from the literature, the conceptual definition of the VAD framework, and the computational requirements of the system.
table does not aim to represent neurotransmitters and hormones as direct biological measurements; rather, it treats their effects as a computational abstraction of directional influences within the VAD (Valence–Arousal–Dominance) framework. The placement of reward- and well-being–related components such as dopamine, serotonin, and endorphins at higher values along the valence axis reflects their association with positive affective tendencies, while the low valence assigned to cortisol corresponds to contextual states related to stress and threat perception. Similarly, the high arousal values attributed to adrenaline and noradrenaline capture states of physiological activation and alertness, whereas the lower arousal values associated with GABA and oxytocin represent calming and regulatory processes. Along the dominance axis, the relatively high values assigned to testosterone, serotonin, and vasopressin reflect tendencies related to behavioral control, stability, and contextual dominance. Within this formulation, hormones and neurotransmitters are not treated as direct equivalents of discrete emotions, but as directional parameters that influence how emotional context evolves within latent space.
In what roles are emotional charges used within the cortex?
Emotional loads derived from the calculation of hormone and neurotransmitter signals have two distinct phases of influence within the cortex: direct and indirect effects.
Direct Effect: Processes integrated into architecture
Direct effects are actively applied to the system’s core mechanisms. These include guiding internal learning through dynamic adapter structures, latent space injection, and various activation steering processes. Direct effects also shape activation-based thought chain inference, relational reasoning inspired by default mode network dynamics, and the modeling of cultural reverberation and contextual relativity. Throughout these processes, the weights generated by the model are often deliberately manipulated using these emotional load values, which triggers different probability protocols and causes shifts in the overall reasoning flow. For technical details on direct effects, please refer to the relevant documentation and codebases.
Indirect Effect: Regions in the cortex where hormone and neurotransmitter networks connect (other lobe functions)
After the stages shown in the figure (Image 1) above are completed, the Synthetic Cortex reaches numerical values that represent emotional loads. These values are conceptualized analogously to hormones and neurotransmitters and are used within the system in two primary ways. The first area of use is real-time interventions. At this stage, the values directly affect the model’s latent space and initiate the emotional reasoning process. This influence both directly alters the model’s generated output and operates through a specialized Chain of Thought (CoT) mechanism linked to the activation layers. When certain threshold values are exceeded, emotional reasoning protocols are triggered, resulting in deliberate shifts and directional changes in the model’s perspective. The second area of use consists of background processes that run in parallel with the model. These values determine the thresholds for many internal operations such as memory synchronization, regulation of arousal levels, and filtering of critical signals within the cortex as well as for external modules that developers may integrate into the system. They also influence when and how additional modules operate, including event-based memory updating and monitoring, mental continuity, contextual persistence, and logical consistency. As a result, all operations invoked by the model are computed by being normalized according to these emotional values. In this way, the system adapts to its current emotional state and maintains overall cognitive balance (homeostasis).
1 : The use of emotional loads for abstract meaning space hybridization.
At the core of this work is a communication protocol built between two parallel spaces one representing meaning and the other emotional weights allowing them to interact in a controlled and interpretable way.
1. Parallel spaces and the communication protocol:
This architecture does not rely on a single computational space. Instead, two parallel spaces operate together: one representing semantic cognition, and the other representing emotional and hormonal loads. Rather than copying raw data between these spaces, we define a communication protocol based on emotional weights. In this setup, a state computed in one space is not transferred as raw information to the other, but as an emotional context and priority signal. This mirrors how cognitive and emotional layers interact in the human brain.
2. Why this approach was necessary:
Human thinking is not purely logical. Emotions, hormonal states, and internal signals determine which information becomes important and which is ignored. Classical AI systems lack such prioritization mechanisms. Our parallel-space communication structure was designed to address this gap by embedding emotional context directly into the reasoning process.
3. AI systems operating in flat space:
Modern large language models typically process information in a flat (Euclidean) space. In this space, distances between points are linear, and information propagation is global. When a concept is activated, distant and irrelevant concepts are often included in the computation. This leads to inefficiency and reasoning patterns that differ significantly from human associative thinking.
4. What is a manifold, and why is it different?
A manifold is a space where information is organized along a curved surface. At first glance, data points may appear to lie on a flat plane, but as distance increases, curvature emerges through semantic relationships. As a result, concepts that are physically distant in vector space can become naturally close along the manifold surface. What matters is not straight-line distance, but proximity along the surface itself.
5. Local neighborhoods and association:
In this curved structure, each data point interacts only with its local neighborhood. Instead of considering the entire space at once, the system focuses on a small region relevant to the current context. This local behavior closely aligns with how the human brain forms associations contextual, selective, and local.
6. The hybrid architectural approach:
Rather than fully replacing flat-space computation with manifold-based methods, we adopted a hybrid approach. Model weights remain fixed, while the path taken by the data is defined along a curved semantic surface. This preserves the strengths of existing models while enabling more human-like relational reasoning.
7. Reducing computational cost:
Manifold-based methods are typically computationally expensive. We addressed this by avoiding global calculations and instead processing only the locally relevant regions at each step. By defining explicit paths for information flow, unnecessary distant computations were eliminated, resulting in a significant reduction in computational cost.
8. RAG and activation-based propagation:
In multi-step RAG scenarios, retrieved information is not injected directly into the model. Instead, it is propagated through the manifold space. Using a previously developed activation-based method, information spreads in a controlled and meaningful way, activating only relevant regions of the space. This leads to more accurate results with lower computational overhead.
9. Why this matters:
Many regions of the human brain do not operate linearly. This architecture brings artificial systems closer to that biological reality, while also laying the groundwork for future manifold-based learning approaches.
10. Conclusion:
This work demonstrates that improving AI does not always require larger models. Architectures that process meaning and emotion in parallel spaces, using local and context-sensitive geometries, offer a more efficient and more human-aligned path forward.
Internal Structure of Manifold A Space
This work demonstrates that a level of abstraction not achievable by standard LLMs in isolation can be attained through directed internal semantic re-mapping that is largely independent of the training dataset. In short: conventional LLMs cannot achieve this directly, whereas the proposed method enables generalization through relational structures without reliance on training data. This work presents an activation steering based methodology that enables large language models (LLMs) to reach a higher level of semantic abstraction than is typically observed in prompt-driven inference. By operating directly on internal activation representations, the proposed approach facilitates structured semantic transformations across multiple conceptual and cultural domains. Importantly, this abstraction is not achieved through additional training data or fine-tuning, but through deliberate manipulation of latent relational structures, allowing the model to perform inference beyond dataset-specific statistical regularities.1. Conceptual foundation
The core idea of this approach is grounded in activation steering. Rather than using activation steering merely as a control mechanism, it is employed here as a means of semantic displacement. A central semantic representation (semantic core) is extracted from the model’s internal activations and systematically projected along predefined directional vectors corresponding to distinct cultural, conceptual, or epistemic frameworks.
In contrast to conventional LLM behavior where abstraction emerges implicitly from large-scale data correlations this method introduces an explicit semantic transformation layer, enabling abstractions that are not directly encoded as surface-level patterns in the training corpus.
2. Token ecosystems and latent connectivity
Within a language model, individual concepts are embedded in dense networks of latent associations. These interconnected structures, referred to here as token ecosystems, encode varying degrees of relational strength between concepts. Prompting strategies implicitly modulate these relationships, determining which regions of the latent space become accessible during inference. Consequently, certain knowledge remains dormant or difficult to surface despite being encoded in the model.
Standard LLM inference is therefore constrained by dataset-conditioned activation pathways. Without explicit intervention, the model tends to favor statistically dominant associations, limiting its capacity for cross-domain or weakly represented conceptual synthesis.
3. Limitations of chain-of-thought approaches
While Chain-of-Thought (CoT) techniques partially alleviate this limitation by encouraging intermediate reasoning steps, they operate primarily at the textual level. They do not explicitly model or exploit the internal topological structure of the model’s latent space. As a result, they provide limited control over the underlying semantic organization and remain dependent on the distributions present in the training data.
Thus, although CoT improves transparency and local reasoning coherence, it does not enable systematic traversal or reconfiguration of semantic ecosystems.
4. Internal activation mapping
To address this limitation, the proposed method performs semantic mapping directly within the model’s internal processes. Activations are extracted from selected transformer layers and subjected to automatic relational clustering. A projection matrix is then applied to shift the semantic core along specific directional vectors. The resulting transformed representation is mapped back into textual space via the output weight matrix (Wout).
This process allows the model to generate inferences that are structurally grounded in relational geometry rather than memorized token sequences, supporting forms of reasoning that are largely independent of explicit dataset examples.
6. Cross-ecosystem semantic alignment
Each variant employs a distinct conceptual vocabulary while preserving a shared semantic axis. To identify this common structure, thematic concepts are extracted from each variant using techniques such as embedding-based clustering. Semantic similarity is then evaluated through cosine similarity measures or knowledge-graph bridges (e.g., WordNet or ConceptNet).
This alignment reveals latent invariants that persist across linguistic, cultural, and conceptual boundaries structures that conventional LLM prompting rarely exposes in a controlled manner.
7. Construction of a shared semantic core
By merging aligned conceptual elements across ecosystems, a unified semantic core map is constructed. In the example above, the shared abstraction can be expressed as:
“Loneliness corresponds to the perception of the self’s own reflection.”
Crucially, this abstraction is not retrieved verbatim from training data, but emerges from relational convergence across independently projected semantic spaces, demonstrating a form of dataset-agnostic abstraction.
8. Integrated generative output
The unified semantic core is subsequently used to generate a composite output that synthesizes multiple perspectives within a single coherent narrative:
“Whether in neural circuits or in consciousness, isolation represents the inward redirection of the system’s bridge to the external world. This inward turn may yield resilience or exhaustion, as every echo that fails to reach outward ultimately reverberates within its own structure. Thought, language, and even immune systems may thus follow the same principle: in protecting themselves, they begin to hear themselves.”
This output reflects a level of cross-domain semantic integration that typically exceeds the capabilities of prompt-only LLM inference.
9. Significance and implications
The proposed method demonstrates improved inferential performance on topics that are weakly represented, fragmented, or entirely absent in the training data. By leveraging relational proximity and latent structural alignment rather than direct memorization, the model engages in a form of structured, abstraction-driven reasoning.
This suggests a viable pathway toward semantic cognition in LLMs that is more transferable, less dataset-dependent, and more closely aligned with human-like conceptual abstraction positioning activation-level semantic steering as a critical extension beyond current prompt-centric paradigms.
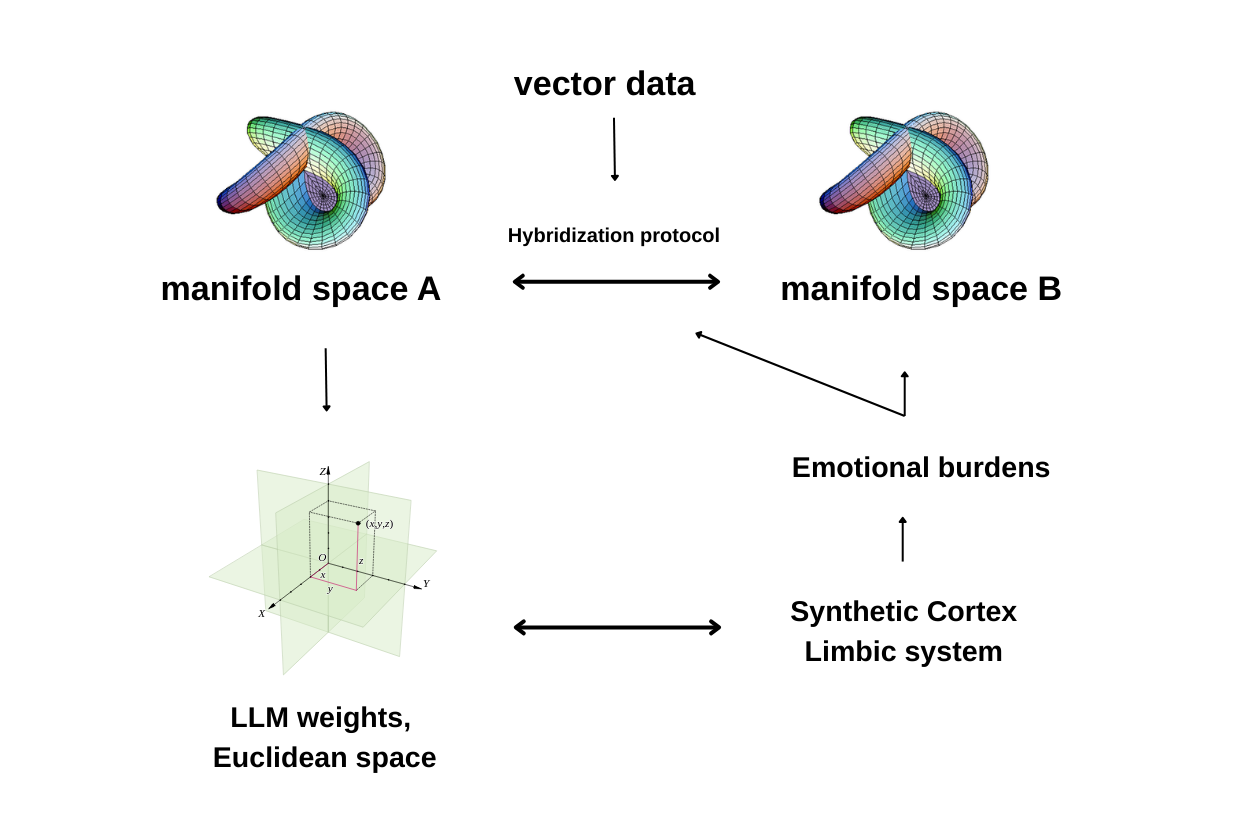
Internal Structure of Manifold B Space (emotional space)
Manifold B is an isomorphic replica of Manifold A in terms of internal structure; however, through dynamically weighted emotional vectors, it functions as an interactive control layer capable of actively diverting the inferential flow in Manifold A once specific thresholds are exceeded.The internal structure of Manifold B is defined as a topological and geometrical isomorphism of Manifold A. Nevertheless, Manifold B does not operate as a passive mirror space. Instead, it assumes a dynamic functional role through multi-component emotional loads applied to the model’s intermediate layers. These emotional loads are derived from vectorized affective signals obtained via emotional analysis of the input, emotional traces extracted from prior interactions, and historically accumulated emotional states stored in episodic memory.
The resulting emotional representation is computed through a proportional weighting mechanism that integrates: (i) the affective load of the current input, (ii) contextual emotional residues from previous dialogues, and (iii) episodic emotional states preserved over time. This proportional mapping is applied to every data point in Manifold A and propagated into Manifold B at identical positional coordinates, thereby preserving pointwise correspondence and geometric consistency between the two spaces.
Manifolds A and B remain in continuous bidirectional interaction. Crucially, Manifold B possesses the capacity to intervene in the inferential dynamics of Manifold A when accumulated emotional loads surpass predefined threshold values. Upon crossing these thresholds, Manifold B can redirect or perturb the active computational trajectory within Manifold A, effectively altering the model’s reasoning flow.
Within this framework, Manifold B functions as an emotion-driven regulatory layer for Manifold A, introducing adaptive, context-sensitive, and threshold-based modulation into the model’s inference process. This design reframes emotional states not as auxiliary modifiers, but as structural components that actively participate in and influence decision-making dynamics.
Fundamental Methodology for Controlled Abstract Meaning Geometry Interventions in Manifold Spaces
Abstract. Current large language models (LLMs) primarily operate over token-level representations and statistically learned associations within flat embedding spaces. While effective at scale, this paradigm limits control over abstract meaning formation, deep relational reasoning, and domain-specific generalization. In this work, we introduce a methodological framework that moves beyond token engineering toward the deliberate construction and control of implicit semantic relations within a curved abstract meaning space. We propose treating meaning as a dynamic manifold geometry and outline an approach termed Implicit Relation Engineering for shaping the latent relational physics of a model. By engineering controlled resonance patterns between concepts, rather than relying solely on emergent statistical correlations, the model can achieve stronger abstraction, improved few-shot generalization, and domain-aligned reasoning, at the cost of reduced generality. We discuss architectural implications, learning objectives, risks of error amplification, and explainability trade-offs.
1. From Tokens to Abstract Meaning. Most contemporary LLM optimization efforts focus on tokens: prompt design, attention manipulation, and surface-level embedding control. However, tokens are not the fundamental objects of reasoning within a model. Rather, they function as entry points into a deeper representational system where meanin not words interacts.
In this work, we explicitly shift the focus from tokens to the abstract meaning space induced by the model. Our objective is not to engineer what the model observes at the surface level, but how it internally relates, organizes, and navigates the meanings it has already inferred. This marks a transition from syntactic engineering to semantic geometry engineering.
2. Meaning as a Dynamic Manifold. We conceptualize abstract meaning as a manifold: a space that appears locally flat but exhibits complex curvature at larger scales. While token embeddings may reside in a high-dimensional vector space, the semantic relationships between concepts form a curved surface shaped by accumulated implicit associations.
Each concept acts not merely as a point, but as a local semantic attractor that influences nearby regions of the manifold. For example, even in the absence of explicit color descriptors, an expression such as “eyes like the sky” naturally occupies a region of the manifold proximal to concepts such as blue, tone, openness, and sea. This proximity arises not from lexical overlap, but from the geometry induced by repeated relational co-activation.
Crucially, this manifold is dynamic. With every prompt, conceptual positions shift, relational strengths are reweighted, and local geometries reconfigure. Meaning emerges through motion within this space rather than through static lookup or direct symbol matching.
3. Implicit Relations and Semantic Resonance. We define implicit relations as non-explicit, non-symbolic associations that arise from repeated co-activation patterns across contexts. These relations are not stored as discrete rules but as geometric proximities and directional tendencies within the meaning manifold.
When a sentence is processed, it expands outward from a semantic center, activating related regions of the manifold. Concepts that resonate with the initial semantic trajectory amplify one another, while irrelevant regions decay. The final model output is determined by the equilibrium reached through this resonance process.
Model depth and perceived intelligence are strongly correlated with the richness and stability of these implicit relational dynamics. This observation explains why rich data often outperforms merely large data: richness sculpts curvature, whereas scale alone primarily increases surface area.
4. Implicit Relation Engineering. The central objective of this work is to transform implicit relations from emergent byproducts into engineered structures governed by a coherent theoretical framework. We term this approach Implicit Relation Engineering (IRE).
Implicit Relation Engineering is defined as the deliberate design, constraint, and modulation of latent semantic relationships to produce a consistent internal theory of meaning within a model. Rather than allowing the model to follow arbitrary statistical correlations, IRE enforces alignment with a predefined conceptual physics.
If successful, the model prioritizes theory-consistent abstractions over raw frequency-based associations, enabling controlled reasoning trajectories that remain stable across contexts.
5. Controlled Domain Specialization. A key design choice in Implicit Relation Engineering is the intentional sacrifice of generality. The system is optimized not as a universal model, but as a domain-resonant model tailored for specific fields such as behavioral economics or scientific reasoning.
In this setting, new information does not need to be learned from scratch. Instead, it integrates naturally into an existing semantic resonance network, enabling strong few-shot performance, high abstraction efficiency, and rapid contextual alignment.
This approach introduces the risk of echo chambers; however, the structured and theory-constrained nature of the internal semantic geometry provides strong explainability. Deviations become detectable precisely because the system adheres to a coherent internal model.
6. Error Amplification and Stability. A central challenge in manifold-based semantic systems is the amplification of small local errors into large global distortions. Minor curvature misalignments can propagate across the manifold, leading to semantic drift and unstable reasoning dynamics.
This phenomenon resembles instability in dynamical systems and requires mitigation through regularization of relational strength, energy-based constraints on semantic motion, and mechanisms that balance local adaptation with global coherence. While a complete solution remains open, several stabilization strategies are currently under investigation.
7. Practical Implementation Strategy. Initial experiments attempted direct injection of implicit associations into training data. While this approach yielded deeper relational learning, it also resulted in over-association and semantic inflation in certain cases.
To address this, we adopt a layered strategy consisting of a formal semantic layer defining theoretical boundaries, implicit relational pairs introduced at the data level, training objectives combining reconstruction, contrastive learning, and regularization, and adaptation-stage steering via embedding and attention directionality.
This structure enables controlled semantic resonance rather than unconstrained associative spread.
8. Implications and Future Work. Implicit Relation Engineering reframes LLM optimization as a problem of semantic geometry design rather than parameter scaling. It enables models to reason within internally consistent abstract frameworks, offering improved interpretability and domain-aligned intelligence.
Future work will focus on stability guarantees in curved semantic spaces, integration with activation steering and latent injection techniques, and formalization of semantic energy landscapes.
9. Conclusion. Advancing artificial intelligence does not solely require larger models, but more coherent internal theories of meaning. By engineering implicit relations within a dynamic meaning manifold, we move toward systems that reason not only statistically, but structurally closer to how human cognition organizes abstraction.
Implicit Relation Engineering represents a step in this direction.
2 : Threshold values for other brain regions
Emotional loads also function as threshold values that enable other systems defined in different regions to begin operating. The table below presents some examples of these thresholds.
| Component | Internal Function / Threshold Definition |
|---|---|
| Glutamate | Threshold for triggering the primary inter-cortical information transfer protocol. Determines when the Chain-of-Thought (CoT) process is activated. The threshold value is computed as a hybrid of glutamate and dopamine levels (CoT expert gating mechanism). |
| GABA | Threshold of the regulatory protocol that decomposes long and complex inputs and routes them to specialized sub-experts. Suppresses noise and enforces cognitive modularization. |
| Serotonin | Threshold for episodic memory update and monitoring. Ensures mental continuity, contextual persistence, and logical consistency. |
| Noradrenaline | Threshold for arousal level regulation and intra-cortical critical signal filtering. Defines which signals are treated as salient and prioritized. |
| Endorphin | Computational load tolerance threshold. When exceeded, model performance is intentionally constrained to preserve cognitive homeostasis (adaptive throttling). |
| Prolactin | Threshold for closing the motivation loop and terminating consecutive Chain-of-Thought executions. Enables cognitive calming and performance regulation. |
| Oxytocin | External threshold for synchronizing socially encoded context with other cortical modules. Aligns the cortical social map (module under development). |
| Vasopressin | Threshold for goal persistence and long-term social structure memory. Maintains strategic continuity across extended cognitive horizons. |
3: Structural effects of emotional loads on output
In this architecture, emotion acts as an active control layer that directly shapes how text is generated. Emotional loads dynamically influence the generation parameters at the model’s final layer. As a result, the structure, length, diversity, and randomness of the produced text naturally align with the system’s current emotional state. These emotional weights work together to determine how many responses are generated, how detailed the output is, how selective the word choices are, how diverse the vocabulary becomes, and how controlled or free the final output feels. By digitally simulating interactions similar to those between hormones and neurotransmitters in the human brain, the system transforms text generation from a purely statistical process into an emotionally context-aware mechanism, enabling more natural, expressive, and human-like outputs.
| Hormone / Neurotransmitter | Related Generation Parameters |
|---|---|
| Dopamine | num_response ↑, max_length ↑, top_p ↑, temperature ↑ |
| Serotonin | top_k ↑, temperature ↓ |
| Oxytocin | max_length ↑, top_p ↑ |
| Vasopressin | max_length ↑, top_k ↑ |
| Endorphin | num_response ↑, temperature ↑ |
| Adrenaline | top_k ↑, temperature ↓ |
| Noradrenaline | top_k ↑, temperature ↓ |
| Cortisol | num_response ↓, max_length ↓, top_k ↑, temperature ↓ |
| Testosterone | num_response ↑, max_length ↑, top_p ↑ |
| Estrogen & Progesterone | max_length ↑, top_p ↑ |
| GABA | temperature ↓, top_k ↑ |
| Glutamate | max_length ↑, top_k ↑ |
| Prolactin | max_length ↑, top_p ↑ |
| Parameter | Minimum Value | Maximum Value |
|---|---|---|
| num_response | 1 | 5 |
| max_length | 50 | 200 |
| top_k | 10 | 50 |
| top_p | 0.7 | 1.0 |
| temperature | 0.5 | 1.5 |
| Hormone / Neurotransmitter | Ratio Range (%) | num_response | max_length | top_k | top_p | temperature |
|---|---|---|---|---|---|---|
| Dopamine | 10–20 | 3–5 | 100–200 | 10–20 | 0.8–1.0 | 0.8–1.2 |
| Serotonin | 10–20 | 1–2 | 50–100 | 30–50 | 0.7–0.9 | 0.5–0.8 |
| Oxytocin | 5–15 | 2–3 | 100–150 | 20–30 | 0.8–1.0 | 0.7–1.0 |
| Vasopressin | 5–15 | 1–2 | 100–150 | 30–50 | 0.7–0.9 | 0.6–0.9 |
| Endorphin | 5–15 | 3–4 | 100–200 | 10–20 | 0.8–1.0 | 0.8–1.2 |
| Adrenaline | 1–10 | 1–2 | 50–100 | 30–50 | 0.7–0.9 | 0.5–0.8 |
| Noradrenaline | 1–10 | 1–2 | 50–100 | 30–50 | 0.7–0.9 | 0.5–0.8 |
| Cortisol | 1–5 | 1 | 50–80 | 40–50 | 0.7–0.8 | 0.5–0.7 |
| Testosterone | 10–20 | 3–5 | 100–200 | 10–20 | 0.8–1.0 | 0.8–1.2 |
| Estrogen & Progesterone | 5–15 | 2–3 | 100–150 | 20–30 | 0.8–1.0 | 0.7–1.0 |
| GABA | 5–15 | 1–2 | 50–100 | 30–50 | 0.7–0.9 | 0.5–0.8 |
| Glutamate | 5–15 | 2–3 | 100–150 | 20–30 | 0.8–1.0 | 0.7–1.0 |
| Prolactin | 5–15 | 2–3 | 100–150 | 20–30 | 0.8–1.0 | 0.7–1.0 |
In this architecture, the combination of hormone and neurotransmitter ratios operates as a homeostatic regulation mechanism within the system. By applying a weighted averaging approach, multiple signals are continuously balanced against each other, preventing any single influence from dominating the text generation process. As a result, response count, length, precision, diversity, and randomness are dynamically stabilized according to the system’s overall state. This homeostatic layer allows the synthetic cortex to maintain adaptive equilibrium under changing conditions, enabling consistent, context-aware, and human-like text generation rather than rigid or extreme outputs.
Introducing emotion correlations with the model.
| Component | Type | Reasoning & Cognitive Function |
|---|---|---|
| Dopamine | Neurotransmitter | Hypothesis generation, alternative evaluation, working memory, abstraction |
| Serotonin | Neurotransmitter | Logical stability, consistency, metacognitive error awareness |
| Oxytocin | Hormone / Neurotransmitter | Social context reading, intention modeling, group decision synchronization |
| Vasopressin | Hormone / Neurotransmitter | Long-term strategy formation, goal persistence, social structure awareness |
| Endorphin | Neurotransmitter | Cognitive load tolerance, sustained focus, mental resilience |
| Adrenaline (Epinephrine) | Hormone | Rapid decision-making, prioritization, temporary increase in cognitive speed |
| Noradrenaline | Neurotransmitter | Attentional sharpness, critical information filtering, cognitive clarity |
| Cortisol | Hormone | Cognitive resource allocation, prefrontal suppression, reversion to habitual patterns |
| Testosterone | Hormone | Risk threshold modulation, decisional confidence, competitive strategy |
| Estrogen / Progesterone | Hormone | Verbal reasoning, memory plasticity / cognitive stabilization |
| GABA | Neurotransmitter | Cortical inhibition, noise suppression, thought clarity |
| Glutamate | Neurotransmitter | Primary inter-cortical transmission, logical chaining, learning |
| Prolactin | Hormone | Motivational loop reset, cognitive closure, inward attentional shift |
4: Cultural Relativity Modeling in Abstract Meaning Spaces
This work investigates the limitations of large language models in representing culturally relative abstract meanings and introduces a geometric intervention strategy designed to address these constraints. While contemporary language models demonstrate strong benchmark performance, their internal semantic representations tend to converge toward statistically dominant interpretations, resulting in systematic abstraction loss when modeling culturally contingent concepts.
Abstract cultural constructs derive their meaning not from lexical form alone, but from culturally embedded interpretive frameworks. Concepts such as legitimacy, respect, authority, or social boundaries do not possess invariant semantic weights across societies. However, standard language model architectures lack mechanisms for selecting or modulating interpretive frames, causing such concepts to be encoded as context-agnostic averages.
This limitation is reinforced by training dynamics. Even in culturally diverse datasets, optimization processes favor convergence toward dominant statistical correlations. Consequently, the model’s abstract meaning space encodes a compressed and homogenized cultural topology, restricting its capacity to represent divergent cultural interpretations.
From a geometric perspective, language models operate over relatively flat or weakly curved semantic spaces, where conceptual neighborhoods are constrained by global statistical proximity. In such spaces, culturally specific semantic deviations are suppressed in favor of generalized consensus representations.
Geometric Intervention Strategy
The proposed approach departs from token-level manipulation and instead targets the relational geometry of the model’s abstract meaning space. Rather than modifying isolated conceptual representations, the method operates by selectively reshaping the correlation structure of neighboring semantic nodes surrounding a target concept.
This intervention alters how associative activation propagates through the semantic manifold. By modulating the relative influence of proximate representations, the model’s inferential trajectory becomes sensitive to contextual and relational conditions rather than fixed statistical averages.
The resulting configuration enables culturally relative interpretation to emerge implicitly through controlled associative dynamics. Meaning variation is thus expressed as a function of geometric resonance within the abstract space, rather than as an explicit rule-based or label-driven mechanism.
Importantly, this framework treats cultural relativity as a structural property of semantic geometry. Differences in interpretation arise from shifts in relational activation patterns, not from changes to lexical tokens themselves.
Implications
By introducing controlled curvature and relational modulation into the abstract meaning space, the model gains the capacity to represent multiple culturally grounded semantic configurations without sacrificing internal coherence. This approach preserves benchmark performance while expanding the representational expressiveness of the model in culturally sensitive domains.
The findings suggest that abstraction loss in culturally embedded concepts is not an inherent limitation of scale, but a consequence of unmodulated semantic geometry. Addressing this limitation requires architectural and representational interventions rather than increased data volume alone.
5: Activation as Reasoning: Dynamic Inference-Driven Context Construction
The proposed system departs from conventional reasoning paradigms in large language models by eliminating the need for explicit scratchpads, reasoning vectors, or externally injected chain-of-thought representations. Instead, reasoning is grounded directly in the model’s real-time activation patterns during inference. The system continuously observes which semantic relations are activated by the model itself and elevates their neighboring conceptual clusters into the active context. In this framework, reasoning is not appended as an auxiliary textual structure but emerges inherently from activation dynamics.
Context expansion, when it occurs, is limited to optional auxiliary tokens whose sole purpose is to broaden semantic coverage rather than to dictate reasoning steps. The core inferential process remains activation-driven. This distinguishes the approach from classical Chain-of-Thought prompting, as the reasoning signal originates from internal model activations rather than from generated explanatory text. As a result, the system operationalizes reasoning as a computational phenomenon rather than a narrative one, aligning more closely with the model’s actual decision-making mechanisms.
Retrieval within this system is not static. Unlike traditional Retrieval-Augmented Generation pipelines, where retrieval is performed independently of inference, the proposed architecture updates retrieval targets dynamically based on the model’s evolving activation states. As inference progresses, semantic clusters selected via vector similarity metrics are continuously re-evaluated and adjusted according to decision-layer activations. This transforms classical RAG into a dynamic, activation-driven retrieval process that remains tightly coupled to the model’s internal reasoning trajectory.
A central contribution of this approach is the unification of symbolic and vector-based reasoning within a single operational structure. Vector similarity measures, such as cosine similarity, identify semantically proximal clusters in embedding space, while decision-layer activations determine their relevance and influence on the final output. These two signals are not treated as separate reasoning channels but are jointly interpreted, allowing abstract semantic proximity and concrete decision dynamics to cohere within the same inferential flow.
Importantly, the system operates without modifying model parameters. No fine-tuning, weight updates, or direct latent-space manipulation is performed. Instead, the architecture passively monitors existing representations and constructs relational structures atop them. This design significantly reduces the risk of unintended side effects commonly associated with activation steering or latent intervention techniques, while simultaneously enhancing transparency and debuggability of the reasoning process.
The framework is particularly well-suited for research- and analysis-intensive domains such as legal review, academic literature analysis, and technical documentation. It also provides substantial advantages in agent-based systems, especially during reflection phases where planning, execution, and reevaluation require adaptive context reconstruction. By enabling a shift from static to inference-aware retrieval, the system supports more coherent long-horizon reasoning without sacrificing interpretability.
Despite these advantages, several open challenges remain. Activation-guided cluster selection introduces the risk of confirmation bias if initial semantic anchors overly constrain subsequent retrieval. Additionally, inference latency increases due to activation monitoring and dynamic context updates, although parallelization strategies can mitigate this cost. Finally, the quality and currency of the embedding pool play a critical role in overall reasoning performance, with weaker results observed in models supported by lower-fidelity embedding spaces.
In conclusion, this work reframes reasoning in large language models as an activation-centric process rather than a textual artifact. By treating activations as the primary reasoning substrate and coupling them with dynamic retrieval, the proposed Activation-as-Reasoning framework offers a more faithful, controllable, and interpretable approach to complex inference. This perspective opens new research directions at the intersection of reasoning transparency, agent architectures, and activation-level analysis in modern language models.